流固耦合的数值模拟算法是计算力学领域中的热点和难点问题。入水问题是一类典型的带有自由界面的流固耦合问题,在航天、航海、国防等领域均有重要的应用背景。
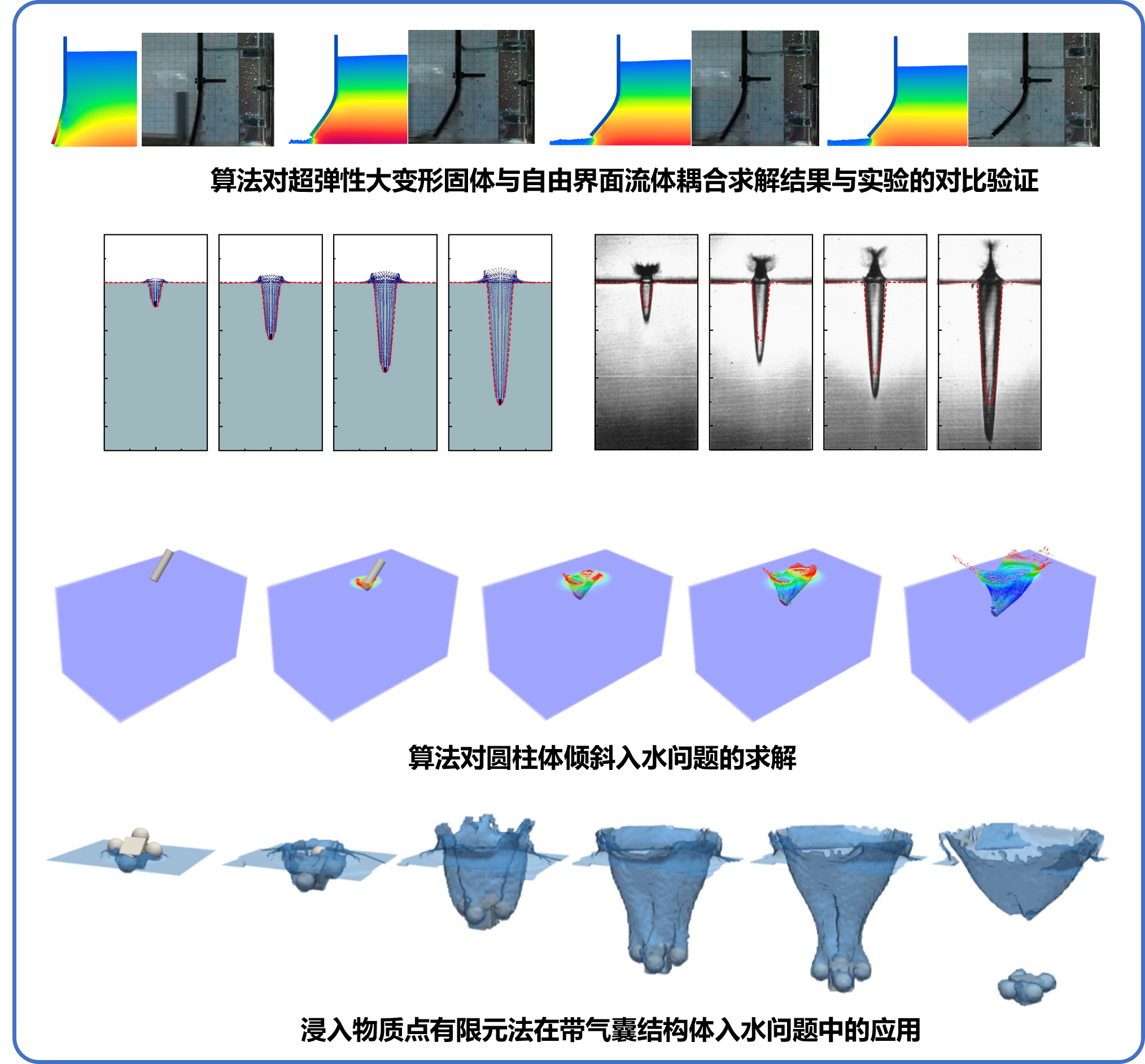
近期,廉艳平教授课题组联合清华大学张雄教授针对自由界面流固耦合问题(特别是入水问题),提出了一种新的数值模拟算法:浸入物质点有限元法(immersed finite element material point, IFEMP)。该算法结合了不可压物质点法、有限元法和浸入边界法的优势,采用欧拉和拉格朗日双重描述,能够高效追踪气、液、固三相界面,并对流体和大变形固体的双向强非线性耦合作用进行精确求解。算法中构建了结合示踪点的网格标记策略,时间复杂度仅为O(n),具有很高的计算效率。同时,通过粒子重整技术有效抑制了数值空泡问题,计算精度和稳定性高。该算法已通过一系列算例验证,包括入水问题、溃坝问题、水流冲击柔性体问题等,并已应用于多个航天实际工程项目中。相关成果以“An immersed finite element material point (IFEMP) method for free surface fluid–structure interaction problems”为题,发表在计算力学顶级期刊《Computer Methods in Applied Mechanics and Engineering》( 2022, 393: 114809. DOI: 10.1016/j.cma.2022.114809)上。